Die Größen der Technik
<< zur NamenslisteEuklid von Alexandria
Euklid von Alexandria ist die als Person am wenigsten greifbare Figur dieser Ausstellung.Leben

Raffael Santi gibt im Bild „Die Philosophenschule von Athen“ Euklid Gestalt, Haltung und Gesicht seines Künstlerkollegen Bramante. Gemalt hat er es 1510/11 in der Stanza della Segnatura für Papst Julius II. Das Fresco zeigt das antike Denken als Wiege der europäischen Kultur, ganz im Geiste der Renaissance.
Über die persönlichen Umstände von Euklid von Alexandria ist nichts bekannt. Weil die Stadt Alexandria jedoch erst im April 331 von Alexander dem Großen („Drei-drei-drei / bei Issos Keilerei“) gegründet wird, kann Euklid nicht in Alexandria geboren worden sein, denn da war er definitiv schon auf der Welt.
Euklid selbst soll sich als aus Ägypten gebürtig bezeichnet haben, anderen zufolge jedoch aus Tyros stammen, einer antiken Hafenstadt im heutigen Libanon und wichtiges Zentrum der Phönizier. Andererseits wird als Geburtsort auch Gela vorgeschlagen, eine dorische Gründung 45 Jahre nach Syrakus, wo ja Archimedes gewirkt hat.
Um 300 v. Chr. verlagert sich das Zentrum wissenschaftlicher und mathematischer Aktivität von Athen nach Alexandrien, wo man viel Wert auf Künste und Wissenschaften legt – man denke nur an die berühmte Bibliothek, mit 700.000 Schriftrollen die größte der antiken Welt. Euklid lehrt am Museion, das entspricht der Universität, Mathematik und gründet die berühmte mathematische Schule von Alexandria, an der später auch Archimedes lernt, oder ist zumindest eines ihrer frühesten Mitglieder. Möglicherweise lebt er am Hofe des Ptolemaios I. Lagi, der auch den Beinamen Soter trägt. Dieser ist einer der Feldherren von Alexander dem Großen und gehört als Statthalter von Ägypten und Libyen zu den Diadochen. Er begründet die Dynastie der Ptolemaeer, die 30 vor Christi von Kleopatra VII („der“ Kleopatra) abgelöst wird.

Fantasieporträt der frühen Neuzeit
Werk
Mit den dreizehn Büchern der "Elemente" tritt uns das erfolgreichste Werk der mathematischen Weltliteratur entgegen: In meisterhafter Darstellung vereinigt Euklid das gesamte mathematische Wissen seiner Zeit und systematisiert es durch die Anordnung nach Axiomen, Definition, Satz, Beweis. 
Papyrusfragment der Stoicheia (Buch II, § 5) aus Oxyrhynchos (P.Oxy. I 29).
Die „Elemente“ Euklids sind nicht die erste Sammlung von Axiomen und ihren logischen Beweisen: Bereits Hippokrates von Chios hat um 430 vor Christi das erste Lehrbuch der Mathematik unter dem Titel „Elemente“ geschrieben, und gleichnamige Titel ähnlichen Inhalts, wahrscheinlich jeweils Verbesserungen des Vorgängers, stammen von Leon (um 380 v. Chr.) und Theudios von Magnesia.

Titelblatt von Henry Billingsleys englischer Übersetzung der Elemente (1570)
Die „Elemente“ sind nicht allein Euklids Wissen und Gedanken, aber Euklid kommt der Verdienst zu, das gesamte mathematische Wissen seiner Zeit gesammelt, geordnet und axiomatisiert zu haben. Euklid ist auch derjenige, der bewiesen hat, dass es unendlich viele Primzahlen gibt.
Die Bücher 1-6 umfassen die Geometrie der Ebene (Planimetrie), die Bücher 7-9 Abhandlungen zur Zahlentheorie (Arithmetik), 10 die irrationale (inkommensurable) Zahlen und 11-13 die Raumgeometrie (Stereometrie). Die Anhänge sind deutlich später hinzugekommen, wobei das 14. Buch dem Hypsikles von Alexandria zugeschrieben wird, dem die Gradeinteilung des Winkels zu verdanken ist (ca. 170 vor Christus).
Die Überlieferungsgeschichte ist ebenso spannend wie verschlungen: Die Nachfrage nach Abschriften der „Stoicheia“ war sehr groß, und so wurde durch händische Vervielfältigung das Lehrbuch nach und nach über den gesamten Mittelmeerraum verbreitet, anzunehmende Abschreibefehler bei Abschriften von Abschriften von Abschriften inklusive. Im 4. nachchristlichen Jahrhundert fügte Theon von Alexandria, Mathematiker am Museion und Herausgeber der „Stoicheia“, Zwischenschritte in der Beweisführung ein und veränderte auch die Sprache. Ein solches Exemplar war weitere 400 Jahre später die Grundlage für die Übersetzung der „Elemente“ ins Arabische. Um 1120 dann wurde eine der arabischen Übersetzungen vom englischen Philosophen Adelard von Bath ins Lateinische übertragen. Weitere 150 Jahre später verglich der italienische Wissenschaftler Campanus von Novara diese Übertragung mit den älteren arabischen Ausgaben und erstellte daraus eine weitere überarbeitete Fassung, die ihrerseits in dieser Version (oder in einer durch Abschrift leicht veränderte) schlussendlich 1482 in Venedig erstmals gedruckt wurde. Seither sind weitere ältere griechische Exemplare aufgetaucht, darunter auch ein vor-Theon-sches. Aus diesen Quellen fertigte der dänische Philosoph Johan L. Heiberg etwa zu der Zeit, als die Alte Technik in der Rechbauerstraße gebaut wurde, eine Übersetzung an, die wahrscheinlich die getreueste Rekonstruktion des Originals ist, die je erreicht wurde.

Allegorische Darstellung der Geometrie, die mit einem Zirkel euklidische Geometrie lehrt. Buchmalerei aus dem 14. Jahrhundert.
Jede mathematische Theorie beruht auf einem derartigen axiomatischen und einem darauf aufbauenden logischen System, mithilfe dessen aus bereits bewiesenen Sätzen neue abgeleitet werden können. Damit ist es Euklids Verdienst, eine streng auf den Methoden der aristotelischen Logik aufbauende Wissenschaft entwickelt zu haben, die zum Vorbild axiomatisch-dekuktiver Wissenschaft wurde.
Parallelenaxiom
Alle Euklidischen Terme, Axiome und Postulate sind kurz und prägnant formuliert. Einzig das Parallelenaxiom (5. Postulat) sticht an Länge und Umständlichkeit aus allen anderen heraus, weshalb man 2000 Jahre lang versuchte, es aus den anderen Axiomen herzuleiten, um es der Schönheit des gesamten Euklidischen Systems willen ersatzlos streichen zu können.Es lautet:
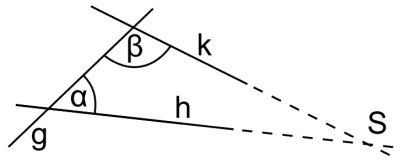
"Gefordert ist, dass wenn eine Gerade g beim Schnitt mit zwei Geraden h und k bewirkt, dass innen auf derselben Seite entstehende Winkel a und ß zusammen kleiner als zwei rechte Winkel werden, dann die zwei geraden Linien h und k bei Verlängerung ins Unendliche sich treffen bei der Seite von g, auf der die Winkel a und ß liegen, die zusammen kleiner als zwei rechte sind."
Eine heute noch gebräuchliche Übertragung dieses 5. Postulats in moderne Form stammt von John Playfair (1795) und lautet: "In einer Ebene a gibt es zu jeder Geraden g und jedem Punkt S außerhalb von g genau eine Gerade, die zu g parallel ist und durch den Punkt S geht."

Carl Friedrich Gauß war der erste, der erkannte, dass dieser Satz nicht aus den anderen hergeleitet werden konnte, ging damit jedoch nicht an die Öffentlichkeit.
Der Kasache Nikolai Iwanowitsch Lobatschewski stellte 1826 eine Geometrie vor, in der alle Axiome Euklids Gültigkeit besitzen mit Ausnahme des 5. Postulats: die nichteuklidische, hyperbolische Geometrie war geboren. Wenig später gelang unabhängig hiervon dem ungarischen Mathematiker Janos Bolyai ein ähnlicher Beweis einer „absolut wahren (hyperbolischen) Geometrie des Raumes.“ In diesem Zusammenhang soll erwähnt werden, dass die gesamte euklidische Geometrie unter Hinfortlassung des 5. Postulats heute als „neutrale Geometrie“ bezeichnet wird, weil ihre Terme, Axiome und Postulate auch im sphärischen und hyperbolischen Raum Gültigkeit haben.
Euklidischer Raum
Dieser Begriff war bis weit ins 19. Jahrhundert hinein gleichbedeutend mit dem physikalischen Raum, der uns umgibt. Erst durch die die Entdeckung des elliptischen und des hyperbolischen Raumes wurde es nötig, den euklidischen gegen andere, nichteuklidische Räume abzugrenzen. Seither kann es in der Raumgeometrie bis zu drei verschiedene Wahrheiten geben: Die Winkelsumme jedes Dreiecks in der euklidischen Ebene beträgt immer 180 Grad, in der elliptischen Geometrie stets mehr, in der hyperbolischen weniger. David Hilbert formuliert im Gegensatz zu Euklid die Grundbegriffe implizit, indem er ausführt, dass wir in drei verschiedenen Systemen denken: in Punkten, Geraden und Ebenen.
Euklidischer Algorithmus
Euklid hat im 7. Buch der Elemente zur Bestimmung des größten gemeinsamen Teilers zweiter Zahlen den sogenannten euklidischen Algorithmus ersonnen, der auf zwei verschiedene Arten schrittweise berechnet werden kann: entweder, man erhält durch „Wechselwegnahme“, also Subtraktion der kleineren von der größeren Zahl, eine Differenz, oder aber man dividiert die größere durch die kleinere Zahl, was eine Zahl mit Rest ergibt, durch den man die kleinere Zahl dividiert, und immer so fort, bis man den größten gemeinsamen Teiler erhält. Dieser Algorithmus liegt heute noch allen Computerprogrammen zugrunde.
